사인-고든 방정식

"오늘의AI위키"는 AI 기술로 일관성 있고 체계적인 최신 지식을 제공하는 혁신 플랫폼입니다.
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.

1. 개요
2. 역사와 어원
3. 정의
- 3.1. 다른 표현
4. 성질
5. 솔리톤 해
6. 양자화
- 6.1. 재규격화 가능성
7. 관련 방정식
8. 응용
참조

1. 개요

사인-고든 방정식은 2차원 시공간에서 정의되는 비선형 편미분 방정식으로, 1862년 에드몽 부르에 의해 처음 연구되었다. 이 방정식은 클라인-고든 방정식의 질량항을 사인 함수 형태의 퍼텐셜로 바꾼 것으로, 솔리톤 해를 가지며 백룬드 변환, 영-곡률 표현 등 다양한 수학적 성질을 갖는다. 사인-고든 방정식은 긴 조셉슨 접합에서의 역학, 결정 전위 모델링, 고전적 XY 모델 등 다양한 물리 시스템을 설명하는 데 활용되며, 양자화된 형태는 띠링 모델과 S-이중성을 통해 관련성을 갖는다.

더 읽어볼만한 페이지

물리학 방정식 - 슈뢰딩거 방정식
슈뢰딩거 방정식은 양자역학에서 시스템의 시간적 변화를 기술하는 기본 방정식으로, 파동 함수에 대한 편미분 방정식이며, 시스템의 총 에너지를 나타내는 해밀토니안 연산자를 포함하고, 양자 상태를 기술하며, 다양한 양자역학적 현상을 설명하는 데 사용된다.
물리학 방정식 - 맥스웰 방정식
맥스웰 방정식은 전기장과 자기장의 상호 작용을 기술하는 네 개의 연립 편미분 방정식으로, 전자기파의 존재와 속도를 예측하여 빛이 전자기파임을 밝히고 고전 전자기학의 기본이 된다.
편미분 방정식 - 나비에-스토크스 방정식
나비에-스토크스 방정식은 유체의 운동을 기술하는 비선형 편미분방정식으로, 질량 및 운동량 보존 법칙에 기반하며, 해의 존재성과 매끄러움은 밀레니엄 문제이지만 다양한 유체 흐름 모델링과 수치 해석적 응용에 활용된다.
편미분 방정식 - 슈뢰딩거 방정식
슈뢰딩거 방정식은 양자역학에서 시스템의 시간적 변화를 기술하는 기본 방정식으로, 파동 함수에 대한 편미분 방정식이며, 시스템의 총 에너지를 나타내는 해밀토니안 연산자를 포함하고, 양자 상태를 기술하며, 다양한 양자역학적 현상을 설명하는 데 사용된다.
수리물리학 - 라플라스 변환
라플라스 변환은 함수 f(t)를 복소수 s를 사용하여 적분을 통해 다른 함수 F(s)로 변환하는 적분 변환이며, 선형성을 가지고 미분방정식 풀이 등 공학 분야에서 널리 사용된다.
수리물리학 - 불확정성 원리
불확정성 원리는 1927년 베르너 하이젠베르크가 발표한 양자역학의 기본 원리로, 입자의 위치와 운동량 등 짝을 이루는 물리량들을 동시에 정확하게 측정하는 것이 불가능하며, 두 물리량의 불확정성은 플랑크 상수에 의해 제한된다.

사인-고든 방정식
개요
유형	비선형 쌍곡선형 편미분 방정식
변수 개수	두 개의 독립 변수
차수	2차
명명법
이름 유래	클라인-고든 방정식과의 유사성, 방정식의 해의 형태
관련 용어	솔리톤, 킹크, 반킹크
방정식
방정식	∂²φ/∂t² - ∂²φ/∂x² = m² sin φ
다른 형태	φ_tt - φ_xx + m² sin φ = 0
변수	φ: 스칼라 장 x, t: 독립 변수 (공간, 시간) m: 상수 (질량)
역사
최초 연구	에드몽 부르 (1862) - 표면 변형 연구
응용	프렌켈-콘토로바 모형 (전위 연구) 자성체 비선형 광학 입자 물리
해법	히로타 료고 (1972) - 솔리톤 해

2. 역사와 어원

1862년에 에드몽 부르(Edmond Bour^프랑스어)가 최초로 연구하였고,^[33] 1939년에 야코프 프렌켈(Яков Ильич Френкель^ru)과 콘토로바(Т. М. Конторова^ru)가 재발견하였다.^[34]

"사인-고든"이라는 이름은 클라인-고든 방정식에 빗댄 말장난인데, 이는 사인고든 방정식이 클라인-고든 방정식 중 질량항을 사인 함수 모양 퍼텐셜로 바꾼 꼴이므로, "클라인"을 각운(脚韻)이 같은 "사인"으로 대체한 것이다.^[4]

3. 정의

2차원 시공간 $(t,x)\in\mathbb R^2$ 에서, '''사인-고든 방정식'''은 다음과 같다.

: $\frac{\partial^2\phi}{\partial t^2}-\frac{\partial^2\phi}{\partial x^2}+\sin\phi=0$

( $\phi=\phi(t,x)$ 를 뜻한다.)

이는 다음과 같은 라그랑지언 밀도로부터 유도할 수 있다.

: $\mathcal L=\frac12\left[\left(\frac{\partial\phi}{\partial t}\right)^2-\left(\frac{\partial\phi}{\partial x}\right)^2\right]-1+\cos\phi$

즉, 퍼텐셜이

: $V(\phi)=1-\cos\phi$

인 스칼라 장론이다. 이는 Bour (1862)에 의한, 이 방정식의 첫 번째 유도이다.

사인-고든 방정식에는 두 가지 동등한 형태가 있는데, 실수 ''시공간 좌표'' $(x,t)$ 로 표기하면, 방정식은 다음과 같다.^[4]

: $\varphi_{tt} - \varphi_{xx} + \sin\varphi = 0,$

여기서 부분 도함수는 아래첨자로 표시된다.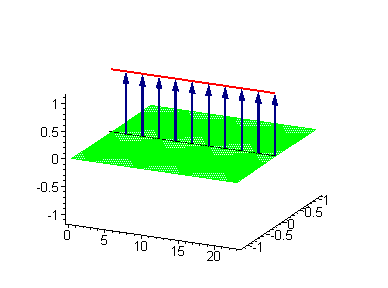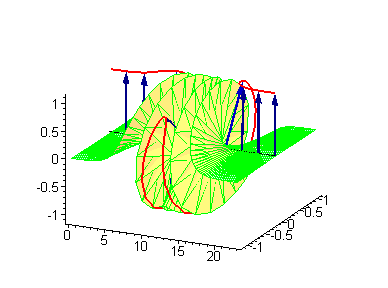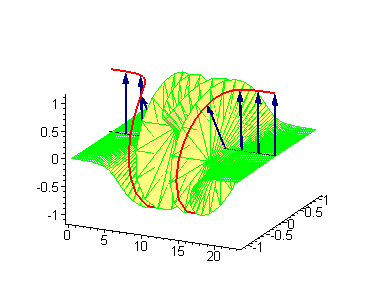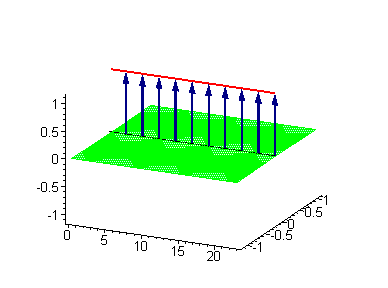

일정한 중력 하에서 일직선으로 매달린 진자 줄을 생각해 보자. 일정한 장력의 끈으로 진자의 추들을 서로 연결한다. 위치

x

에서의 진자 각도를

\varphi

라고 하면, 개략적으로 진자 줄의 역학은 뉴턴의 제2법칙을 따르는데, 시간과 거리를 적절하게 조정하면 사인-고든 방정식이 된다.^[7]

"사인-고든 방정식"이라는 이름은 물리학의 잘 알려진 클라인-고든 방정식에 대한 말장난이다.^[4]

사인-고든 방정식은

\mathbb{R}^2

상의 특정

\mathfrak{su}(2)

-접속의 곡률이 0과 같다는 것과 동일하다.^[12]

'''사인-고든 방정식'''(

\sinh

방정식)은 다음과 같다.^[13]

:

\varphi_{xx} - \varphi_{tt} = \sinh\varphi.

또 다른 밀접하게 관련된 방정식은 '''타원 사인-고든 방정식''' 또는 '''유클리드 사인-고든 방정식'''이다.

:

\varphi_{xx} + \varphi_{yy} = \sin\varphi,

여기서

\varphi

는 이제 변수 ''x''와 ''y''의 함수이다. 이것은 더 이상 솔리톤 방정식이 아니지만, 해석적 연속 (또는 윅 회전) ''y'' = i''t''에 의해 사인-고든 방정식과 관련되어 많은 유사한 속성을 갖는다.

'''타원 sinh-고든 방정식'''은 유사한 방식으로 정의될 수 있다.

또 다른 유사한 방정식은 리우빌 장론의 오일러-라그랑주 방정식에서 나온다.

\varphi_{xx} - \varphi_{tt} = 2e^{2\varphi}.

일반화는 토다 장론에 의해 주어진다.^[14]

3. 1. 다른 표현

실수 시공간 좌표

(x, t)

대신 광원추 좌표

(u, v)

를 사용하면, 사인-고든 방정식은 다음과 같이 표현할 수 있다.^[5]

:

\varphi_{uv} = \sin\varphi.

이는 가우스 곡률 ''K'' = -1인 곡면, 즉 유사구면을 연구하는 과정에서 고려되었던 사인-고든 방정식의 원래 형태이다.

4. 성질

사인-고든 방정식은 19세기에 가우스 곡률이 -1인 유사구면을 연구하는 과정에서 처음 고려되었다.^[5] 이 방정식은 다음과 같은 두 가지 형태로 나타낼 수 있다.

실수 시공간 좌표 ( $x, t$ ):

::

\varphi_{tt} - \varphi_{xx} + \sin\varphi = 0,

^[4]

광원추 좌표 ( $u, v$ ):

::

\varphi_{uv} = \sin\varphi.

^[5]

여기서

u = \frac{x + t}{2}, \quad v = \frac{x - t}{2}

이다.

유사구면에서 점근선 사이의 각도를

\varphi

라고 하면, 곡면의 제1 기본 형식은

::

ds^2 = du^2 + 2\cos\varphi \,du\,dv + dv^2,

이며, 제2 기본 형식은

L = N = 0, M = \sin \varphi

이다. 가우스-코다치 방정식은

\varphi_{uv} = \sin\varphi

이 된다.^[5]

사인-고든 방정식의 해는 강체 변환을 통해 고유하게 유사구면을 결정할 수 있다. 이를 '곡면의 기본 정리'라고도 부른다.

사인-고든 방정식은 진자 줄의 움직임을 묘사하는 데에도 사용될 수 있다. 일정한 중력 하에 일직선으로 매달린 진자 줄에서, 위치

x

에서의 진자 각도를

\varphi

라고 하면, 진자 줄의 역학은 뉴턴의 제2법칙을 따른다.

:

\underbrace{m\varphi_{tt}}_{\text{질량 곱하기 가속도}} = \underbrace{T \varphi_{xx}}_{\text{장력}} - \underbrace{mg \sin\varphi }_{\text{중력}}

이를 시간과 거리를 적절하게 조정하면 사인-고든 방정식을 얻을 수 있다.^[7]

4. 1. 백룬드 변환

\phi_1

이 사인-고든 방정식을 만족하는 해이면 아래 공식을 통해 또 다른 해

\phi_2

를 구할 수 있다.

:

\frac{\partial\phi_2}{\partial t}=\frac{\partial\phi_1}{\partial x}+\left(a-\frac1a\right)\cos\frac{\phi_1}2\sin\frac{\phi_2}2+\left(a+\frac1a\right)\sin\frac{\phi_1}2\cos\frac{\phi_2}2

:

\frac{\partial\phi_2}{\partial x}=\frac{\partial\phi_1}{\partial t}+\left(a+\frac1a\right)\cos\frac{\phi_1}2\sin\frac{\phi_2}2+\left(a-\frac1a\right)\sin\frac{\phi_1}2\cos\frac{\phi_2}2

(※ a는 상수)

위 공식은 아래 식들을 통해 만들어진다.

:

\left(\frac{\partial}{\partial x}+\frac{\partial}{\partial t}\right)(\phi_2-\phi_1)=2a\sin\frac{\phi_2+\phi_1}2

:

\left(\frac{\partial}{\partial x}-\frac{\partial}{\partial t}\right)(\phi_2+\phi_1)=\frac2a\sin\frac{\phi_2-\phi_1}2

이 방정식과 관련된 의사구면 표면 변환에 대한 19세기의 비안키와 백룬드의 연구는 백룬드 변환의 발견으로 이어졌다.^[6] 의사구면 표면의 또 다른 변환은 1879년 소푸스 리가 도입한 리 변환으로, 사인-고든 방정식의 해에 대한 로렌츠 부스트에 해당한다.^[6]

새로운 표면을 생성하지는 않지만, 새로운 해를 구성하는 데 더 간단한 방법도 있다. 사인-고든 방정식은 홀수이므로, 모든 해의 음수는 또 다른 해이다. 그러나 이것은 표면의 법선 방향 선택으로 귀결되므로 새로운 표면을 제공하지 않는다. 해를 이동하여 새로운 해를 찾을 수 있다. 즉,

\varphi

가 해이면,

\varphi + 2n\pi

(

n

은 정수)도 해이다.

사인-고든 방정식의 해가

\varphi

라고 가정하자.

:

\varphi_{uv} = \sin \varphi.\,

다음 시스템

:

\begin{align}\psi_u & = \varphi_u + 2a \sin \Bigl( \frac{\psi+\varphi}{2} \Bigr) \\\psi_v & = -\varphi_v + \frac{2}{a} \sin \Bigl( \frac{\psi-\varphi}{2} \Bigr)\end{align} \,\!

여기서 ''a''는 임의의 매개변수이며, 사인-고든 방정식을 만족하는 함수

\psi

에 대해 풀 수 있다. 이는 자동-Bäcklund 변환의 예시인데,

\varphi

와

\psi

둘 다 사인-고든 방정식과 같은 방정식의 해이기 때문이다.

행렬 시스템을 사용하면, 사인-고든 방정식의 해에 대한 선형 Bäcklund 변환을 찾을 수도 있다.

예를 들어,

\varphi

가 자명한 해

\varphi \equiv 0

이면,

\psi

는 솔리톤에 적용된 부스트와 관련된

a

를 갖는 1-솔리톤 해이다.

4. 2. 위상 전하와 에너지

위상 전하 또는 회전수는 해

\varphi

에 대해 다음과 같이 정의된다.

:

N = \frac{1}{2\pi} \int_\mathbb{R} d\varphi = \frac{1}{2\pi} \left[\varphi(x = \infty, t) - \varphi(x = -\infty, t)\right].

해

\varphi

의 에너지는 다음과 같다.

:

E = \int_\mathbb{R}dx \left(\frac{1}{2}( \varphi_t^2 + \varphi_x^2) + m^2(1 - \cos\varphi)\right)

여기서 퍼텐셜이 음수가 되지 않도록 상수 에너지 밀도가 추가되었다. 이름 섹션에서 언급했듯이, 이를 통해 퍼텐셜의 테일러 전개의 처음 두 항은 질량 스칼라장의 퍼텐셜과 일치하며, 고차 항은 상호작용으로 간주할 수 있다.

위상 전하는 에너지가 유한하면 보존된다. 위상 전하는 로렌츠 부스트까지 고려하더라도 해를 결정하지 못한다. 자명한 해와 솔리톤-반솔리톤 쌍의 해는 모두

N = 0

을 갖는다.

4. 3. 영-곡률 표현

사인-고든 방정식은

\mathbb{R}^2

상의 특정

\mathfrak{su}(2)

-접속의 곡률이 0과 같다는 것과 동일하다.^[12]

구체적으로,

\mathbb{R}^2

상의 좌표

(u,v)

에 대해 접속 성분

A_\mu

는 다음과 같다.

A_u = \begin{pmatrix}i\lambda & \frac{i}{2}\varphi_u \\ \frac{i}{2}\varphi_u & -i\lambda\end{pmatrix} = \frac{1}{2}\varphi_u i\sigma_1 + \lambda i\sigma_3,

A_v = \begin{pmatrix}-\frac{i}{4\lambda}\cos\varphi & -\frac{1}{4\lambda}\sin\varphi \\ \frac{1}{4\lambda}\sin\varphi & \frac{i}{4\lambda}\cos\varphi\end{pmatrix} = -\frac{1}{4\lambda}i\sin\varphi\sigma_2 - \frac{1}{4\lambda}i\cos\varphi\sigma_3,

여기서

\sigma_i

는 파울리 행렬이다.

그러면 영-곡률 방정식

\partial_v A_u - \partial_u A_v + [A_u, A_v] = 0

은 사인-고든 방정식

\varphi_{uv} = \sin\varphi

와 동일하다. 영-곡률 방정식은

F_{\mu\nu} = [\partial_\mu - A_\mu, \partial_\nu - A_\nu]

로 정의될 경우 곡률이 0과 같다는 것과 일치하므로 그렇게 명명되었다.

행렬 쌍

A_u

와

A_v

는 또한 영-곡률 방정식이 락스 방정식을 만족하는 대신 편미분 방정식을 복구한다는 의미에서 사인-고든 방정식에 대한 락스 쌍으로 알려져 있다.

5. 솔리톤 해

사인-고든 방정식은 솔리톤 해를 갖는다.^[6] 초기 위치가 $x_0$ 이고 속도가 $v$ 인 솔리톤은 다음과 같이 표현된다.

: $\phi(t,x)=4\arctan\exp\left(\frac{x-x_0-vt}{\sqrt{1-v^2}}\right)$

19세기 비안키와 백룬드는 이 방정식과 관련된 의사구면 표면 변환을 연구하여 백룬드 변환을 발견했다. 소푸스 리는 1879년 리 변환을 도입했는데, 이는 사인-고든 방정식의 해에 대한 로렌츠 부스트에 해당한다.^[6]

사인-고든 방정식의 해가 주어졌을 때, 그 해의 음수나 $2n\pi$ ( $n$ 은 정수)를 더한 값도 해가 된다.

5. 1. 1-솔리톤 해

사인-고든 방정식의 흥미로운 특징은 솔리톤 및 멀티솔리톤 해의 존재이다. 1-솔리톤 해는 다음과 같이 표현된다.^[6]

:

\varphi_\text{soliton}(x, t) := 4 \arctan \left(e^{m \gamma (x - vt) + \delta}\right),

여기서

:

\gamma^2 = \frac{1}{1 - v^2},

이다. 좀 더 일반적인 형태의 방정식은 다음과 같다.

:

\varphi_{tt} - \varphi_{xx} + m^2 \sin\varphi = 0.

\gamma

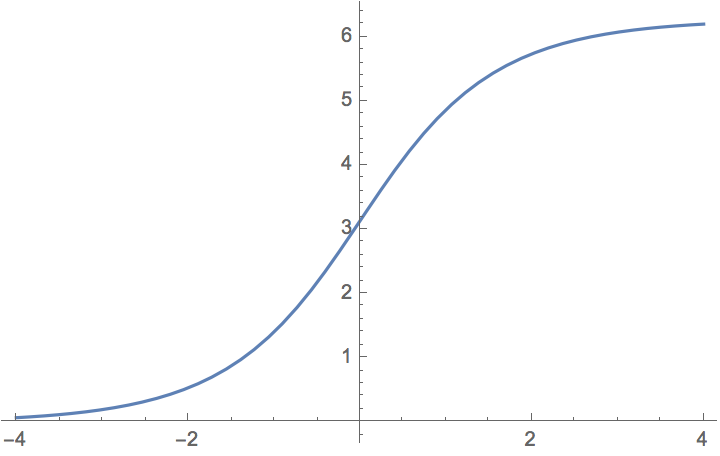
에 대해 양의 근을 선택한 1-솔리톤 해는 '''킨크'''라고 불리며, 변수

\varphi

에서 시스템을 하나의 상수 해

\varphi = 0

에서 인접한 상수 해

\varphi = 2\pi

로 이동시키는 비틀림을 나타낸다.

\varphi \cong 2\pi n

인 상태는 에너지 0의 상수 해이므로 진공 상태라고 한다.^[6]

\gamma

에 대해 음의 근을 취하는 1-솔리톤 해는 '''안티킨크'''라고 불린다. 1-솔리톤 해의 형태는 자명한(진공) 해에 대한 백룬드 변환을 적용하고 결과적인 1차 미분을 적분하여 얻을 수 있다.^[6]

1-솔리톤 해는 1970년 Julio Rubinstein이 도입한 탄성 리본 사인-고든 모델을 사용하여 시각화할 수 있다.^[8] 탄성 리본의 시계 방향(왼손잡이) 비틀림을 위상 전하

\theta_\text{K} = -1

을 갖는 킨크로 간주한다. 위상 전하

\theta_\text{AK} = +1

을 갖는 시계 반대 방향(오른손잡이) 비틀림은 안티킨크가 된다.^[6]

5. 2. 2-솔리톤 해

2-솔리톤 해는 1-솔리톤 해에 백클룬드 변환을 반복 적용하여 얻을 수 있다.^[10] 사인-고든 방정식의 2-솔리톤 해는 솔리톤의 특징을 보이는데, 이동하는 킨크 및/또는 안티킨크는 서로를 통과하며, 이때 유일하게 관찰되는 효과는 위상 변화이다. 충돌하는 솔리톤은 속도와 모양을 유지하므로, 이러한 상호작용을 탄성 충돌이라고 한다.^[9]

킨크-킨크 해는 다음과 같다.

:

\varphi_{K/K}(x,t) = 4 \arctan \left(\frac{v \sinh \frac{x}{\sqrt{1 - v^2}}}{\cosh \frac{vt}{\sqrt{1 - v^2}}}\right)

킨크-안티킨크 해는 다음과 같다.

:

\varphi_{K/AK}(x,t) = 4 \arctan \left(\frac{v \cosh \frac{x}{\sqrt{1 - v^2}}}{\sinh \frac{vt}{\sqrt{1 - v^2}}}\right)

--

브리더는 결합된 킨크-안티킨크 쌍으로 진동하는 형태를 갖는 2-솔리톤 해이다.^[11] 세 가지 유형의 브리더가 존재한다.^[11]

정지 브리더:

:

\varphi(x,t) = 4 \arctan\left(\frac{\sqrt{1-\omega^2}\;\cos(\omega t)}{\omega\;\cosh(\sqrt{1-\omega^2}\; x)}\right).

--

이동하는 킹크와 정지한 브리더 또는 이동하는 안티킹크와 정지한 브리더 간의 3-솔리톤 충돌은 정지한 브리더의 위상 이동을 초래한다. 이동하는 킹크와 정지한 브리더 간의 충돌 과정에서, 브리더의 이동 $\Delta_\text{B}$ 는 다음과 같이 주어진다.

: $\Delta_\text{B} =\frac{2\operatorname{artanh}\sqrt{(1 - \omega^2)(1 - v_\text{K}^2)}}{\sqrt{1 - \omega^2}},$

여기서 $v_\text{K}$ 는 킹크의 속도이고, $\omega$ 는 브리더의 주파수이다. 만약 정지한 브리더의 이전 위치가 $x_0$ 라면, 충돌 후 새로운 위치는 $x_0 + \Delta_\text{B}$ 가 된다.

--

5. 3. 3-솔리톤 해

이동하는 킹크와 정지한 브리더 또는 이동하는 안티킹크와 정지한 브리더 간의 3-솔리톤 충돌은 정지한 브리더의 위상 이동을 초래한다. 이동하는 킹크와 정지한 브리더 간의 충돌 과정에서, 브리더의 이동

\Delta_\text{B}

는 다음과 같이 주어진다.

:

\Delta_\text{B} =\frac{2\operatorname{artanh}\sqrt{(1 - \omega^2)(1 - v_\text{K}^2)}}{\sqrt{1 - \omega^2}},

여기서

v_\text{K}

는 킹크의 속도이고,

\omega

는 브리더의 주파수이다. 만약 정지한 브리더의 이전 위치가

x_0

라면, 충돌 후 새로운 위치는

x_0 + \Delta_\text{B}

가 될 것이다.

6. 양자화

사인-고든 모형은 양자화할 수 있다.^[35] 양자화하면 플랑크 상수에 해당하는 매개변수가 추가되어 입자 스펙트럼이 달라진다. 이 모형의 산란 행렬은 해석적으로 계산 가능하며, 티링 모형과 S-이중성을 통해 동형이다.^[36]

양자장론에서 사인-고든 모델은 플랑크 상수와 동일시될 수 있는 매개변수를 포함한다. 입자 스펙트럼은 솔리톤, 반솔리톤, 그리고 유한한(또는 0) 수의 브리더로 구성된다.^[17]^[18]^[19] 브리더의 수는 매개변수의 값에 따라 달라진다. 다중 입자 생성은 질량 껍질 위에서 상쇄된다.

사인-고든 모델의 반고전적 양자화는 루드비히 파데예프와 블라디미르 코레핀에 의해 수행되었다.^[20] 정확한 양자 산란 행렬은 알렉산더 자몰로드치코프에 의해 발견되었다.^[21] 이 모델은 콜먼이 발견한 S-이중성을 통해 띠링 모델과 동형이다.^[22]

6. 1. 재규격화 가능성

양자장론에서 사인-고든 모델은 플랑크 상수와 동일시될 수 있는 매개변수를 포함한다. 양자 사인-고든 방정식은 지수가 꼭짓점 연산자가 되도록 수정되어야 한다.

:

\mathcal{L}_{QsG} = \frac{1}{2} \partial_\mu \varphi \partial^\mu \varphi + \frac{1}{2}m_0^2\varphi^2 - \alpha(V_\beta + V_{-\beta})

여기서

V_\beta = :e^{i\beta\varphi}:

이고, 세미콜론은 정규 순서를 나타낸다. 가능한 질량 항이 포함된다.

\beta^2

매개변수의 값에 따라 재정규화 가능성이 달라진다.^[23] 이 영역은 위르크 프뢸리히가 발견했다.

'''유한 영역''': $\beta^2 < 4\pi$ 인 영역으로, 이론을 잘 정의하기 위해 반대항이 필요하지 않다.
'''초재정규화 가능 영역''': $4\pi < \beta^2 < 8\pi$ 인 영역으로, 유한한 수의 반대항이 필요하다. 각 임계값 $\frac{n}{n+1}8\pi$ 를 넘을 때마다 더 많은 반대항이 필요하다.^[24]
$\beta^2 > 8\pi$ 인 경우: 이 이론은 정의되지 않는다.

경계 값은

\beta^2 = 4\pi

과

\beta^2 = 8\pi

이며, 각각 콜먼 대응을 통해 이론이 자유 페르미온에 이중적인 자유 페르미온 점과 정점 연산자가 아핀 sl₂ 부분 대수를 형성하고 이론이 엄격하게 재정규화 가능한 (재정규화 가능하지만 초재정규화 가능하지 않은) 자기 쌍대점이다.

7. 관련 방정식

실수 시공간 좌표 $(x,t)$ 에서 사인-고든 방정식은 다음과 같이 표현된다.^[4]

: $\varphi_{tt} - \varphi_{xx} + \sin\varphi = 0,$

여기서 부분 도함수는 아래첨자로 표시된다. 광원추 좌표 $(u, v)$ (여기서 $u = \frac{x + t}{2}, \quad v = \frac{x - t}{2}$ )를 사용하면, 사인-고든 방정식은 다음과 같은 형태를 갖는다.^[5]

: $\varphi_{uv} = \sin\varphi.$

이는 19세기에 가우스 곡률이 -1인 유사구면을 연구하는 과정에서 고려되었던 사인-고든 방정식의 원래 형태이다.

'''신-고든 방정식'''(sinh-Gordon equation)은 다음과 같다.^[13]

: $\varphi_{xx} - \varphi_{tt} = \sinh\varphi.$

'''타원 사인-고든 방정식'''(elliptic sine-Gordon equation)은 다음과 같다.

: $\varphi_{xx} + \varphi_{yy} = \sin\varphi,$

여기서 $\varphi$ 는 변수 ''x''와 ''y''의 함수이다. 이 방정식은 윅 회전 ''y'' = i''t''를 통해 사인-고든 방정식과 관련된다.

리우빌 장론의 오일러-라그랑주 방정식은 다음과 같다.

: $\varphi_{xx} - \varphi_{tt} = 2e^{2\varphi}.$

토다 장론은 사인-고든 방정식의 일반화이다.^[14] 리우빌 장론은 유한 Kac–Moody 대수 $\mathfrak{sl}_2$ 에 대한 토다 장론이고, sin(h)-고든은 아핀 Kac–Moody 대수 $\hat \mathfrak{sl}_2$ 에 대한 토다 장론이다.

8. 응용

사인-고든 방정식은 결정 전위를 모델링하는 프렌켈-콘토로바 모델의 연속 극한으로 나타난다.^[7]

긴 조셉슨 접합에서의 역학은 사인-고든 방정식으로 잘 설명되며, 반대로 사인-고든 모델을 연구하기 위한 유용한 실험 시스템을 제공한다.^[27]

사인-고든 모델은 자성을 모델링한 고전적 XY 모델의 연속 쿨롱 가스에서 와류와 반-와류의 유효 작용과 동일한 보편성 부류에 속하며, 와류에 대한 코스터리츠-사울리스 전이는 사인-고든 장론의 재규격화군 분석을 통해 도출할 수 있다.^[28]^[29]^[30]^[31]

사인-고든 방정식은 또한 양자 하이젠베르크 모델, 특히 XXZ 모델의 형식적인 연속 극한으로도 나타난다.^[32]

참조

_[1] 논문 Theorie de la deformation des surfaces https://gallica.bnf.[...]
_[2] 논문 On the theory of plastic deformation and twinning
_[3] 논문 Exact Solution of the Sine-Gordon Equation for Multiple Collisions of Solitons 1972-11
_[4] 서적 Solitons and Instantons: An Introduction to Solitons and Instantons in Quantum Field Theory North-Holland
_[5] 서적 Handbook of Nonlinear Partial Differential Equations Chapman & Hall/CRC Press
_[6] 논문 Geometry of solitons https://www.ams.org/[...]
_[7] 간행물 The sine-Gordon Model: General Background, Physical Motivations, Inverse Scattering, and Solitons https://link.springe[...] Springer International Publishing 2023-11-17
_[8] 논문 Sine-Gordon equation
_[9] 논문 Neuronic system inside neurons: molecular biology and biophysics of neuronal microtubules http://cogprints.org[...]
_[10] 서적 Bäcklund and Darboux Transformations: Geometry and Modern Applications in Soliton Theory Cambridge University Press
_[11] 웹사이트 Solitons and Soliton Collisions http://homepages.tve[...] Miroshnichenko A. E., Vasiliev A. A., Dmitriev S. V.
_[12] 서적 Solitons, instantons, and twistors Oxford University Press 2010
_[13] 서적 Handbook of Nonlinear Partial Differential Equations CRC Press 2011-12-16
_[14] 논문 A unified method for solving sinh-Gordon–type equations 2006-02
_[15] 논문 The sine-Gordon and sinh-Gordon equations on the circle
_[16] 논문 The complex sine-Gordon model on a half line
_[17] 논문 Direct calculation of the S matrix in the massive Thirring model
_[18] 논문 The Quantum Sine-Gordon Model and the Fermi-Bose Relation
_[19] 논문 Structure of the vacuum in the quantum sine-Gordon model
_[20] 논문 Quantum theory of solitons
_[21] 논문 Relativistic factorized S-matrix in two dimensions having O(N) isotopic symmetry
_[22] 논문 Quantum sine-Gordon equation as the massive Thirring model https://journals.aps[...] 2023-01-27
_[23] arXiv Local operators in the Sine-Gordon model: $\partial_μϕ\, \partial_νϕ$ and the stress tensor 2022
_[24] arXiv The dynamical sine-Gordon model in the full subcritical regime 2018
_[25] 논문 The Dynamical Sine-Gordon Model https://link.springe[...] 2023-05-14
_[26] 논문 Supersymmetric extension of the sine-Gordon theory with integrable boundary interactions
_[27] 서적 The sine-Gordon Model and its Applications: From Pendula and Josephson Junctions to Gravity and High-Energy Physics https://link.springe[...] Springer International Publishing 2023-08-22
_[28] 논문 Sine-Gordon theory and the classical two-dimensional x − y model 1976-11-15
_[29] 논문 Classical and quantum statistical mechanics in one and two dimensions: Two-component Yukawa — and Coulomb systems http://projecteuclid[...] 1976-10
_[30] 논문 Renormalization Group Theory of the Interfacial Roughening Transition 1978-08-01
_[31] 논문 An introduction to lattice gauge theory and spin systems 1979-10-01
_[32] arXiv How Algebraic Bethe Ansatz works for integrable model 1996
_[33] 저널 인용 Théorie de la déformation des surfaces http://gallica.bnf.f[...]
_[34] 저널 인용
_[35] 저널 인용
_[36] 저널 Quantum sine–Gordon equation as the massive Thirring model 1975

본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.

문의하기 : help@durumis.com